Rappresentazione dell'Informazione - Lezione in semi-presenza
Lezione in semi-presenza
7. Sommare in differenti rappresentazioni numeriche
Tra la rappresentazione decimale e quella binaria c’è una similarità. Questa similarità ci aiuta?
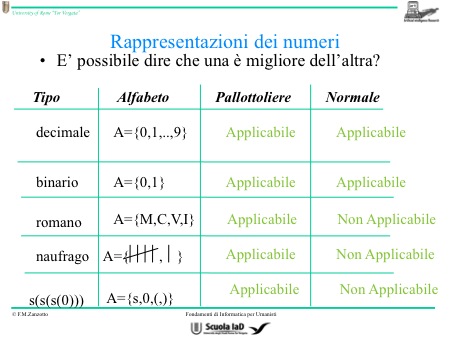
Tornando all’algoritmo della somma e al metodo del pallottoliere, vediamo che si può applicare ai numeri decimali, ai numeri binari, ma anche ai numeri romani e ai numeri del naufrago. Allora passiamo al metodo “ normale” e vediamo che esso è applicabile soltanto al sistema dei numeri decimali e al sistema binario.
Perciò si è trovata la risposta alla domanda: perché i numeri romani sono caduti in disgrazia. L’algoritmo migliore per fare la somma è quello “ normale” perché per svolgerlo impieghiamo meno tempo. Siccome l’algoritmo “normale” non si può applicare ai numeri romani, questi sono destinati a perire.
Così come vengono rappresentati, infatti, non consentono l’applicazione dell’algoritmo, quindi non centra nulla il fatto che il popolo romano venne battuto e l’impero romano d’occidente cadde con l’arrivo dei barbari. Anche i cinesi e i giapponesi che hanno un altro alfabeto, quindi lettere diverse, usano gli stessi nostri numeri decimali perché questo sistema consente di fare i calcoli più rapidamente.
Abbiamo capito che esistono dei numeri che possiamo usare per fare i calcoli. Se questi numeri sono costruiti in una determinata maniera, i conti vengono bene, altrimenti i conti non sono facili da risolvere.
Per i numeri posizionali e decimali possiamo dire che, data la conformazione del numero, la cifra vale sempre quel valore secondo la posizione in cui si trova. Lo stesso non si può dire per i numeri romani. Questa tipologia di numeri non è necessariamente decimale, la decimalità è vera solo per i numeri che conosciamo e dipende dal numero di cifre che abbiamo nel nostro alfabeto.
Anche i numeri binari si comportano allo stesso modo ed è per questo che, anche a questi numeri, si può applicare l’algoritmo della somma. Al contrario, per i numeri romani e per i numeri del naufrago, questo non è possibile.
De Saussure fu un importante linguista che, tra le altre cose, ci ha dato la libertà di poter scegliere una qualsiasi rappresentazione dei nostri oggetti. Infatti, per lui, non c’è nessuna ragione per la quale le cose si debbano chiamare con il nome che gli è stato dato per convenzione (la mucca che si chiama mucca…).
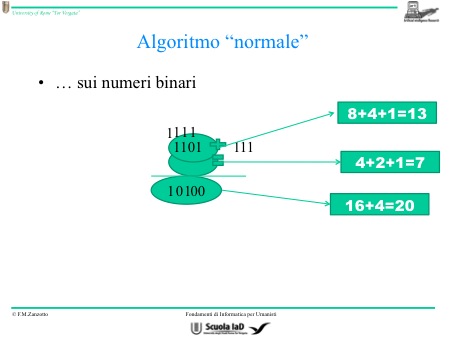
L’alfabeto dei numeri binari è 0 e 1. dati due numeri binari, proviamo a sommarli quindi:
1 1 1 1 +
1 0 1
_______
La prima colonna da dove comincio la somma è quella più a destra, quella cioè che considero attiva. Abbiamo 1 + 1 che sarebbe uguale a 2, ma non bisogna dimenticarsi che stiamo sommando numeri binari. Potrebbe fare 1 e riporto 1. in realtà è come se stessimo sommando 9 e 1 che sarebbe 10, ma scrivo solo lo 0 e riporto di 1.
Nell’alfabeto a dieci, quando non si può scrivere un numero perché troppo grande, si torna indietro. Nel caso di 1 e 0, il numero subito precedente (bisogna tornare indietro) è 0. perciò la somma tra 1 e 1 è 0, ma il riporto lo scrivo alla colonna subito successiva a sinistra. Stesso discorso vale anche per la colonna successiva dove dovremo tornare indietro e, ogni volta che torniamo indietro, abbiamo il riporto.
Anche per questa seconda colonna il risultato è 0 perché dovevo sommare 1 + 0 + 1 che riportavo. Alla colonna successiva ho 1 + 1 + 1 che riportavo e il risultato è 1. e poi ho l’ultima colonna in cui ho solo 1, ma con l’altro 1 che riportavo è 0, davanti a questo 0, però, scrivo anche 1 perché non posso riportarlo da nessuna parte. Quindi il risultato completo di quest’addizione è 1 0 1 0 0.
Quella appena usata è una nuova procedura; la procedura che usavamo per i numeri decimali, la applichiamo anche ai numeri binari, e lavoriamo come se stessimo lavorando con i decimali, solo che si tratta di numeri binari e quindi si comportano in modo differente.
La stessa procedura si può provare ad applicarla anche ai numeri romani, ma non si ottiene nessun risultato soddisfacente.
Per capire se il procedimento è corretto, trasformiamo il tutto in numeri decimali.
Per tradurre un numero decimale da una base a un’altra base (base 10 casualmente), si prende la posizione che diventa l’esponente di quanti elementi abbiamo alla base e si ottengono i valori delle posizioni. Fatto ciò, prendiamo il numero che sta nella posizione e lo moltiplichiamo per il valore e poi sommiamo tutti. Alla fine abbiamo 20. Quindi, applicare la stessa procedura che applicavamo per i numeri posizionali decimali sui numeri posizionali binari, fa ottenere i risultato dovuto.
Ora vediamo i numeri ternari, abbiamo tre cifre: 0 1 2. sommiamo due numeri ternari: 121 (che non è centoventuno perché siamo in ternaria) + 12. senza inventare un altro lessico chiameremo questi due numeri uno due uno e uno due.
Dovendo fare questa somma in ternario, cominciamo sempre dal mettere in colonna e dal partire dalla colonna più a destra. 1 + 2 = 0 con il riporto di 1, poi, passando ala colonna immediatamente a sinistra facciamo 2 + 1 che sarebbe 0, ma riportavo 1 e quindi fa 1. ed in ultimo scrivo il 2. quindi il risultato di tutta l’operazione è 210.
Pur liberandoci dell’accidente storico per il quale noi contiamo in base 10, abbiamo visto che manteniamo la capacità di fare operazioni con le procedure e gli stessi algoritmi che valevano per i numeri decimali. Quindi la capacità di fare operazioni non dipende dalla decimalità del numero, ma dalla posizionalità.
Inoltre, sia lo 0 che 1 che 2, anch’essi è un accidente che valgano 0 1 e 2.
Nella base binaria è accidentale che si usino 0 e 1, infatti, all’interno dei calcolatori, vengono usati valori di elettricità diversi da 0 e 1, questi simboli corrispondono solo a due valori di elettricità.
In base ternaria, quanto fa 2 + 2? Il risultato è 11 (non undici ma uno uno).
Abbiamo capito perché i numeri romani sono caduti in disuso, perché, non essendo posizionali, non possono essere sommati con l’algoritmo “ normale”.
Abbiamo anche capito perché l’algoritmo del pallottoliere è peggiore dell’algoritmo “ normale”, e cioè perché è meno veloce.
Il fatto che l’algoritmo normale sia veloce è la somma di due fattori: la velocità stessa dell’algoritmo, ma anche da come rappresenta il numero, perché l’algoritmo normale funziona solo per alcune rappresentazioni del numero. E cioè per la modalità posizionale, perché tutto dipende dal mettere i numeri in colonna.