Rappresentazione dell'Informazione - Lezione in semi-presenza
| Site: | Università di Tor Vergata for UNWTO |
| Course: | Fondamenti di informatica per il turismo |
| Book: | Rappresentazione dell'Informazione - Lezione in semi-presenza |
| Printed by: | Guest user |
| Date: | Wednesday, 4 March 2026, 6:58 AM |
Description
Lezione in semi-presenza
1. Rappresentazione: essenza
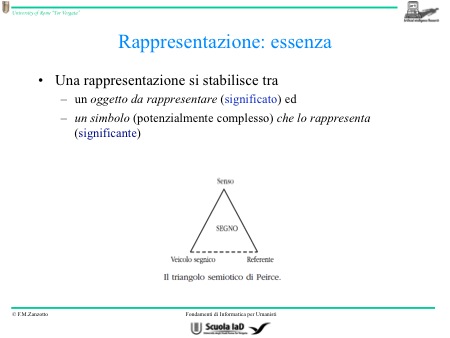
Cos’è la rappresentazione? Parlando di rappresentazione bisogna far riferimento ad altri due concetti. Ciò che si rappresenta e l’elemento con cui lo rappresentiamo. L’oggetto da rappresentare può esser chiamato significato, mentre il simbolo semplice o complesso che lo rappresenta può venir chiamato significante. Possono essere chiamati con il nome di significante e significato.
Mario è un nome, ma è anche un simbolo che ci serve per parlare di quella determinata persona.
Oltre al significante e al significato, c’è un terzo elemento che è l’immagine mentale che noi abbiamo di questa persona. Questo terzo elemento prende il nome di senso. Il senso è quello che uno ha in testa che serve per parlare di un individuo specifico.
Guardando due figure diverse: la prima con degli uomini che suonano (la tromba…) e la seconda con una sola nota musicale, comprendiamo immediatamente che una (la prima) è più espressiva perché ci da l’informazione sulla musica che si sta suonando addirittura (musica jazz). Entrambi sono simboli, ma li differenzia l’espressività.
Il significante è il simbolo, il significato è il referente.
Altro elemento da prendere in esame è l’arbitrarietà: vediamo due figure di cani di razze diverse. In italiano questi animali si chiamano cani, ma in inglese si chiamano dogs e così via (hanno un nome diverso per ogni lingua). Tutte le parole sono delle convenzioni, ma perché si è scelta proprio questa parola per indicare questo animale? Non c’è nessuna ragione per la quale quest’animale si chiama cane. Tranne alcuni rarissimi casi, non c’è nessuna parola che ha ragion d’essere, in qualsiasi lingua, si tratta di convenzioni (come affermano anche i linguisti).
Le convenzioni basta stabilirle e comunicarle.
Neppure le onomatopeiche hanno una ragione d’esistere poiché si differenziano tra un Paese e gli altri.
Questo è un vantaggio perché se le parole non hanno nessuna regola per esistere, possiamo cambiarle e crearne delle nuove, basta che ci si mette d’accordo (si era tentato di creare un linguaggio universale). L’unica parola uguale in tutte le lingue è “ mamma”.
2. Introduzione
Il secondo MATTONCINO-BASE è la rappresentazione dell’informazione:
Abbiamo visto gli algoritmi e i parametri o variabili. Abbiamo codificato gli algoritmi usando il linguaggio con cui comunichiamo ogni giorno (linguaggio naturale che per noi è l’italiano).
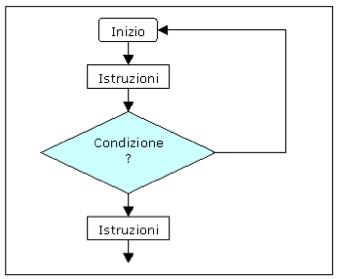
Successivamente, abbiamo visto che esistono delle regolarità e abbiamo deciso di indicare il “ se” in modo diverso, così abbiamo introdotto i diagrammi di flusso. Ma non abbiamo codificato nulla; si è semplicemente introdotto un simbolo per rappresentare delle tipologie di istruzioni canoniche. Abbiamo imbrigliato poco il linguaggio introducendo:
- i rettangoli (istruzioni);
- il rombo (condizioni);
- le frecce (indicante il flusso).
Se è possibile, come si possono codificare queste informazioni?
Per questo dobbiamo capire com’è possibile rappresentare l’informazione e cosa dobbiamo usare per farlo.
Tutto ciò che è rappresentabile è alfabetizzabile attraverso un numero e tutto ciò che è rappresentabile attraverso un numero, è rappresentabile attraverso una cifra binaria.
Cosa ci interessa rappresentare in un algoritmo per produrre una macchina in grado di elaborarlo?
Alla fine di questo MATTONCINO saremo in grado di rispondere alla domanda Perché i numeri romani sono entrati in disuso? E saremo in grado di verificare che 2 + 2 = 11.
3. Linguaggio naturale: problemi e possibilità
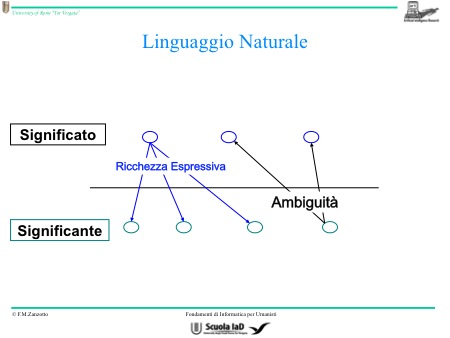
Il linguaggio naturale è quello che noi usiamo tutti i giorni che ha due fenomeni importantissimi: ricchezza espressiva e ambiguità.
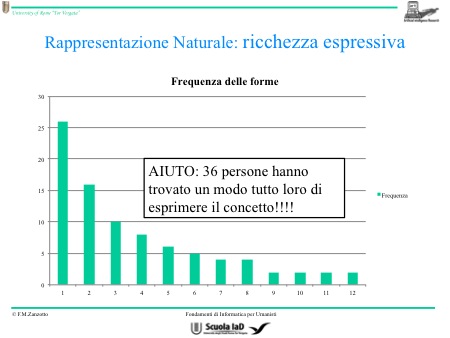
Avendo un concetto in testa, si può esprimere in diversi modi e verrà compreso ugualmente (esempio delle mail). Se ordiniamo le forme rispetto alla frequenza decrescente, si osserva che la prima forma è il doppio della seconda, la seconda è il doppio della terza (legge di decadimento delle forme o legge di Zift).
Da ciò si deduce che il linguaggio naturale è un linguaggio molto ricco perché, dato un concetto, lo si può scrivere in molteplici modi.
Importante, in una lingua naturale, è anche il fattore ambiguità. Parlando di uomo, ad esempio, vengono in mente diverse cose:
- essere umano di sesso maschile
- uomo in senso generico inteso sia per la donna sia per l’uomo maschio.
- Uomo nel senso di adulto e non bambino.
- L’uomo è stupido inteso come la razza maschile (o umanità?)
- L’uomo si sta distruggendo (umanità intera)…
Esempio con imposta. L’uomo era solo sostantivo, mentre imposta passa da un ambito all’altro (participio passato, nome, …).
Sarà una caratteristica delle parole singole quella di non discernere da un significato all’altro? No: è una caratteristica proprio delle lingue storico-naturali.
Infatti, se prendiamo la frase “la borsetta di pelle di nonna”, vediamo che le parole non cambiano significato, ma l’imbarazzo è strutturale poiché sta nel come mettiamo le parole insieme, non si tratta di un imbarazzo che deriva dalle singole parole.
Osserviamo che, partendo da un unico significante, ci si può riferire a più significati (ambiguità). Partendo da più significanti, vediamo che possono ricondurre a un solo significato (ricchezza espressiva). Quindi, ora possiamo dire che non è vero che esiste una relazione chiara tra tutti i significanti e i significati. Se li prendiamo singolarmente la situazione è chiara, ma complessivamente entra l’ambiguità.
In linguistica questi fenomeni si chiamano sinonimia e polisemia.
Vediamo due tipi di rappresentazione: iconica e simbolica che in informatica sono similari all’analogica e alla digitale.
La rappresentazione iconica consiste in un disegno che raffigura ciò che vogliamo rappresentare (ci vorrebbero molte parole per descriverla). Lo stop è una rappresentazione sia iconica che simbolica perché dentro c’è la scritta. La rappresentazione simbolica è quella fatta attraverso dei simboli affiancabili (componibili).
La rappresentazione analogica è la trasposizione della rappresentazione iconica, mentre la rappresentazione digitale è la trasposizione della rappresentazione simbolica.
4. Cosa si vuole rappresentare in un algoritmo?
Si vogliono rappresentare i dati e le istruzioni (cosa vogliamo fare). Per farlo scegliamo la rappresentazione simbolica in quanto è l’unica che ci consente di giustapporre simboli l’uno all’altro, perciò si può dire che sia componibile.
E’ possibile rappresentare tutto con i numeri? Se ciò fosse possibile avremo bisogno solo di due numeri ovvero lo 0 e 1 (codice binario)?
Se esistono dei simboli essi sono ordinabili. Una volta ordinati possono essere associati a dei numeri.
Un numero deve essere composto di cifre che devono essere messe in sequenza. Per parlare dei numeri usiamo un codice formato da cifre (0 1 2…).
Esistono modi differenti per rappresentare i numeri. Alcuni hanno come alfabeto di cifre quelli che abbiamo visto. Esistono dei significati che sono i valori dei numeri e sono staccati dai significanti.
Esiste una funzione che ci permette di passare dal significante al significato e questa funzione la chiamiamo valore.
La scorsa volta avevamo visto l’ambiguità e la ricchezza espressiva, entrambe caratteristiche delle lingue storico-naturali.
Per poter fare delle cose con un linguaggio e volendo dare un ordine con questo linguaggio, bisogna che il linguaggio in questione non sia ambiguo. Perciò occorre inventarsi un modo per parlare non ambiguamente.
Quindi, mentre l’ambiguità è un vero problema quando si parla con la macchina, la ricchezza espressiva è un “arricchimento” perché l’importante è non essere ambigui, se poi il concetto o l’input da dare alla macchina lo si esprime in diversi modi, questo non è un problema. Anzi, è un vantaggio avere la ricchezza espressiva perché si esprime lo stesso concetto in diversi modi secondo chi lo deve sentire.
Uno degli scopi dell’informatica è costruire lingue che siano non ambigue.
5. Proprietà dei numeri: la rappresentazione simbolica scelta
Si è detto che per rappresentare occorre un significante e un significato. Dobbiamo scegliere il significante (il simbolo con cui rappresentare); questo significante lo si può scegliere come lo si vuole perché, per nessuna ragione esistente, il significante è attaccato al significato (si tratta soltanto di convenzioni).
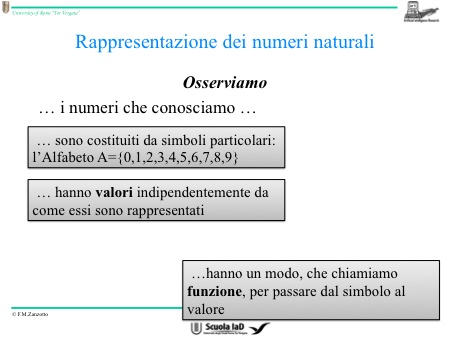
Il significante che scegliamo sono i numeri perché essi hanno proprietà interessanti. Una di queste proprietà è: qualsiasi cosa che è numerabile può essere raccontata attraverso i numeri (ad esempio l’alfabeto, occorre solo scegliere l’ordine delle lettere).
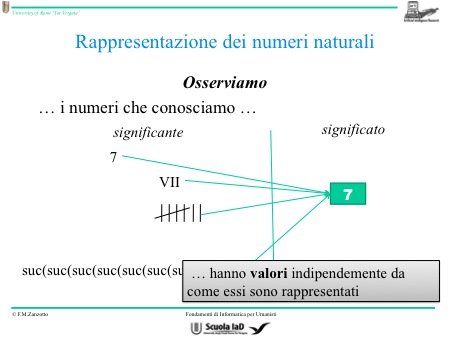
I numeri sono giustapposizioni di simboli particolari. I numeri hanno valori indipendenti rispetto al modo come sono scritti: il mondo dei valori è il mondo dei concetti, è ciò che vogliamo rappresentare.
Il numero che si osserva, 75, è un modo diverso per dire “ settantacinque”. Scrivere 7 e 5 è già diverso dal dire “ settantacinque”. Il valore è sempre 75.
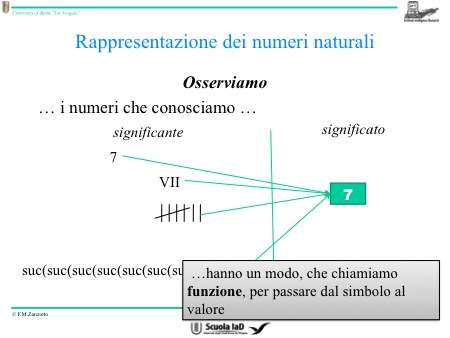
Il modo che ci consente di passare dalla rappresentazione ai valori è la funzione che è costituita da regole particolari.
La funzione la chiamiamo val e sappiamo come lavora perché possiamo prendere il numero e attribuirgli un valore: 37 vale “ trentasette” caramelle. Non è scritto “ trentasette”, ma è scritto il valore rappresentabile di “ trentasette”, ma “ trentasette” si può rappresentare in diversi modi, ma di questi modi, il più naturale per noi è quello decimale per il quale si rappresenta così: 37.
Il problema nasce dato il fatto che per rappresentare bisogna trasferire il significato su un simbolo, perciò, quel simbolo scelto rappresenta solo il significato (è come se lì ci fosse il significato). Questa funzione, però, non è uguale per tutte le rappresentazioni (la decimale, quella del naufrago…).
6. Numeri decimali e posizionali
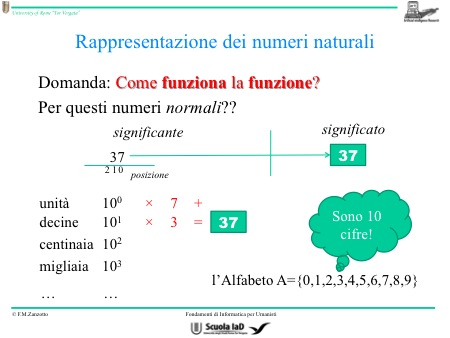
Come si rappresenta la funzione con il numero decimale? Il numero decimale è composto di unità, decine e così via. Per questa funzione bisogna contare i numeri successivi.
Dato che esistono le unità, le decine, le centinaia e…, bisogna calcolare quanto valgono tutte: l’unità vale 1 e così via… perciò, se si pone il 7 di 37 nelle unità, questo numero si leggerà come “ sette”. Il suo valore, infatti, è ottenuto dal fatto che si trova nella posizione delle unità e dal fatto che è “ sette”. La stessa cosa vale per le decine: se prendiamo il 3 di 37 e lo posizioniamo nelle decine, ha il suo valore moltiplicato per 10 in quanto si trova nella posizione delle decine (3 x 10 = 30), quindi il valore di quel numero è 30.
Quindi, la funzione dei numeri decimali è: prendiamo 1 (il valore delle unità) e lo moltiplichiamo per il numero che troviamo nella posizione delle unità (in questo caso 7), poi si moltiplica il valore delle decine (10) per il valore che si trova nella posizione delle decine (in questo caso 3). Il numero che si ottiene in questo caso facendo questo procedimento è 37.
Se determiniamo la posizione, il valore dell’elemento unità, decine, centinaia…, è un numero particolare elevato alla posizione. Partendo dalla posizione 0 che corrisponde alla posizione delle unità, la posizione 1 corrisponde alle decine, la posizione 2 corrisponde alle centinaia, la posizione 3 corrisponde alle migliaia ecc.
La cifra vale valori differenti secondo la posizione in cui si trova.
Perché si ripete il numero 10 (10 elevato alla 0 per la posizione delle unità, 10 elevato alla 1 per la posizione delle decine…)? 10 è il numero delle cifre, ogni cifra, infatti, vale 10 elevato al numero che corrisponde alla posizione in cui si trova.
Questo sistema è legato all’alfabeto, perciò possiamo cambiare il numero di cifre che vogliamo utilizzare, basta che i numeri seguano le stesse regole.
Abbiamo cambiato la base che da 10 è divenuta 2 e interpretiamo il numero 101: 2 elevato alla 0 per la posizione delle unità; 2 elevato alla 1 per le posizioni delle decine; 2 elevato alla 2 per la posizione delle centinaia…
L’alfabeto permette di cambiare la cardinalità. 1 moltiplicato per 2 elevato alla 0 che è 1 è uguale a1; poi moltiplichiamo 0 per 2 elevato alla 1 che è 2, è uguale a 0; poi moltiplichiamo 1 per 2 alla seconda che è 4 e il risultato è 4. perché il significato è 5?
Il valore al numero lo si da come lo si legge. Possiamo cambiare la base poiché i numeri sono legati all’alfabeto. Ma se avessimo B cifre nell’alfabeto, potremo fare lo stesso ragionamento?
Sì. Ci sono popoli che contano in base 24 perché non usano solo le dita delle mani come noi che, infatti, contiamo in base 10. perciò, quella di contare in base 10 è un’imposizione sul sistema, ma il sistema funziona lo stesso se scegliamo un’altra base.
Il caso generale è Val(….) =…
Dato un qualsiasi numero, anche lunghissimo, avrà sempre n cifre. Nel leggere tale numero, già gli si assegna un valore perché lo si legge in decimale, i numeri per quanto lunghi non possono essere infinitamente lunghi. Perciò n è il numero di cifre che compongono il numero.
Nella sommatoria aggiungiamo un nuovo elemento, ovvero i che è un numero generico che può variare tra 0 e n. supponendo che n = 4, i potrà assumere un valore compreso tra 0 e 4. Ciò indica che si possono sommare tutti i numeri da 0 a 4. Perciò i è una variabile che può rappresentare un numero qualunque tra questi.
Partendo da I = 0, vogliamo sommare tutti quei dati per arrivare a I = n. si tratta di una somma di tanti numeri che scriviamo con S (sommatoria).
Per qualsiasi base contenuta nell’alfabeto, si può passare dal significato al significante, avendo una qualsiasi sequenza di simboli.
I numeri che possiamo pensare, sono una qualsiasi sequenza di cifre che vengono descritte da un insieme. La funzione valore funziona in questo modo.
Ciò che abbiamo fatto fin’ora non vale per tutti i numeri, c’è una modalità specifica per ognuno.
Qual è la funzione val?
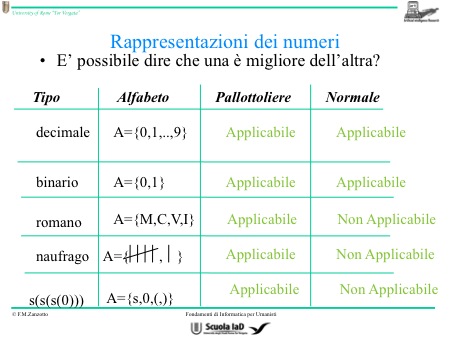
Per il sistema decimale e per il sistema binario va bene quella vista fin’ora. L’alfabeto, invece, è diverso per ogni numero (naufrago, romano…): decimale A= (0,1, …, 9); binario A = (0,1); romano A = (V, M, c, X, I); naufrago A = (diverso). Il romano e il naufrago sono simili.
Nelle prime due rappresentazioni qualsiasi sequenza di cifre è un numero, cosa che non vale per i numeri romani che sono sequenze di lettere, ma non è che ogni sequenza di lettere rappresenta un numero, e lo stesso anche per il naufrago.
7. Sommare in differenti rappresentazioni numeriche
Tra la rappresentazione decimale e quella binaria c’è una similarità. Questa similarità ci aiuta?
Tornando all’algoritmo della somma e al metodo del pallottoliere, vediamo che si può applicare ai numeri decimali, ai numeri binari, ma anche ai numeri romani e ai numeri del naufrago. Allora passiamo al metodo “ normale” e vediamo che esso è applicabile soltanto al sistema dei numeri decimali e al sistema binario.
Perciò si è trovata la risposta alla domanda: perché i numeri romani sono caduti in disgrazia. L’algoritmo migliore per fare la somma è quello “ normale” perché per svolgerlo impieghiamo meno tempo. Siccome l’algoritmo “normale” non si può applicare ai numeri romani, questi sono destinati a perire.
Così come vengono rappresentati, infatti, non consentono l’applicazione dell’algoritmo, quindi non centra nulla il fatto che il popolo romano venne battuto e l’impero romano d’occidente cadde con l’arrivo dei barbari. Anche i cinesi e i giapponesi che hanno un altro alfabeto, quindi lettere diverse, usano gli stessi nostri numeri decimali perché questo sistema consente di fare i calcoli più rapidamente.
Abbiamo capito che esistono dei numeri che possiamo usare per fare i calcoli. Se questi numeri sono costruiti in una determinata maniera, i conti vengono bene, altrimenti i conti non sono facili da risolvere.
Per i numeri posizionali e decimali possiamo dire che, data la conformazione del numero, la cifra vale sempre quel valore secondo la posizione in cui si trova. Lo stesso non si può dire per i numeri romani. Questa tipologia di numeri non è necessariamente decimale, la decimalità è vera solo per i numeri che conosciamo e dipende dal numero di cifre che abbiamo nel nostro alfabeto.
Anche i numeri binari si comportano allo stesso modo ed è per questo che, anche a questi numeri, si può applicare l’algoritmo della somma. Al contrario, per i numeri romani e per i numeri del naufrago, questo non è possibile.
De Saussure fu un importante linguista che, tra le altre cose, ci ha dato la libertà di poter scegliere una qualsiasi rappresentazione dei nostri oggetti. Infatti, per lui, non c’è nessuna ragione per la quale le cose si debbano chiamare con il nome che gli è stato dato per convenzione (la mucca che si chiama mucca…).
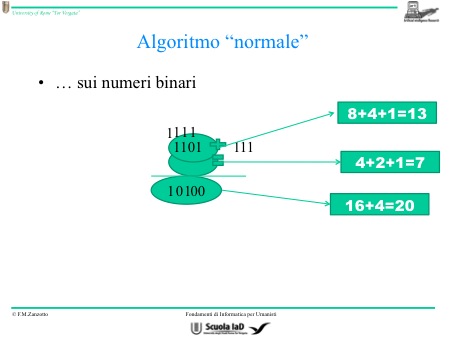
L’alfabeto dei numeri binari è 0 e 1. dati due numeri binari, proviamo a sommarli quindi:
1 1 1 1 +
1 0 1
_______
La prima colonna da dove comincio la somma è quella più a destra, quella cioè che considero attiva. Abbiamo 1 + 1 che sarebbe uguale a 2, ma non bisogna dimenticarsi che stiamo sommando numeri binari. Potrebbe fare 1 e riporto 1. in realtà è come se stessimo sommando 9 e 1 che sarebbe 10, ma scrivo solo lo 0 e riporto di 1.
Nell’alfabeto a dieci, quando non si può scrivere un numero perché troppo grande, si torna indietro. Nel caso di 1 e 0, il numero subito precedente (bisogna tornare indietro) è 0. perciò la somma tra 1 e 1 è 0, ma il riporto lo scrivo alla colonna subito successiva a sinistra. Stesso discorso vale anche per la colonna successiva dove dovremo tornare indietro e, ogni volta che torniamo indietro, abbiamo il riporto.
Anche per questa seconda colonna il risultato è 0 perché dovevo sommare 1 + 0 + 1 che riportavo. Alla colonna successiva ho 1 + 1 + 1 che riportavo e il risultato è 1. e poi ho l’ultima colonna in cui ho solo 1, ma con l’altro 1 che riportavo è 0, davanti a questo 0, però, scrivo anche 1 perché non posso riportarlo da nessuna parte. Quindi il risultato completo di quest’addizione è 1 0 1 0 0.
Quella appena usata è una nuova procedura; la procedura che usavamo per i numeri decimali, la applichiamo anche ai numeri binari, e lavoriamo come se stessimo lavorando con i decimali, solo che si tratta di numeri binari e quindi si comportano in modo differente.
La stessa procedura si può provare ad applicarla anche ai numeri romani, ma non si ottiene nessun risultato soddisfacente.
Per capire se il procedimento è corretto, trasformiamo il tutto in numeri decimali.
Per tradurre un numero decimale da una base a un’altra base (base 10 casualmente), si prende la posizione che diventa l’esponente di quanti elementi abbiamo alla base e si ottengono i valori delle posizioni. Fatto ciò, prendiamo il numero che sta nella posizione e lo moltiplichiamo per il valore e poi sommiamo tutti. Alla fine abbiamo 20. Quindi, applicare la stessa procedura che applicavamo per i numeri posizionali decimali sui numeri posizionali binari, fa ottenere i risultato dovuto.
Ora vediamo i numeri ternari, abbiamo tre cifre: 0 1 2. sommiamo due numeri ternari: 121 (che non è centoventuno perché siamo in ternaria) + 12. senza inventare un altro lessico chiameremo questi due numeri uno due uno e uno due.
Dovendo fare questa somma in ternario, cominciamo sempre dal mettere in colonna e dal partire dalla colonna più a destra. 1 + 2 = 0 con il riporto di 1, poi, passando ala colonna immediatamente a sinistra facciamo 2 + 1 che sarebbe 0, ma riportavo 1 e quindi fa 1. ed in ultimo scrivo il 2. quindi il risultato di tutta l’operazione è 210.
Pur liberandoci dell’accidente storico per il quale noi contiamo in base 10, abbiamo visto che manteniamo la capacità di fare operazioni con le procedure e gli stessi algoritmi che valevano per i numeri decimali. Quindi la capacità di fare operazioni non dipende dalla decimalità del numero, ma dalla posizionalità.
Inoltre, sia lo 0 che 1 che 2, anch’essi è un accidente che valgano 0 1 e 2.
Nella base binaria è accidentale che si usino 0 e 1, infatti, all’interno dei calcolatori, vengono usati valori di elettricità diversi da 0 e 1, questi simboli corrispondono solo a due valori di elettricità.
In base ternaria, quanto fa 2 + 2? Il risultato è 11 (non undici ma uno uno).
Abbiamo capito perché i numeri romani sono caduti in disuso, perché, non essendo posizionali, non possono essere sommati con l’algoritmo “ normale”.
Abbiamo anche capito perché l’algoritmo del pallottoliere è peggiore dell’algoritmo “ normale”, e cioè perché è meno veloce.
Il fatto che l’algoritmo normale sia veloce è la somma di due fattori: la velocità stessa dell’algoritmo, ma anche da come rappresenta il numero, perché l’algoritmo normale funziona solo per alcune rappresentazioni del numero. E cioè per la modalità posizionale, perché tutto dipende dal mettere i numeri in colonna.