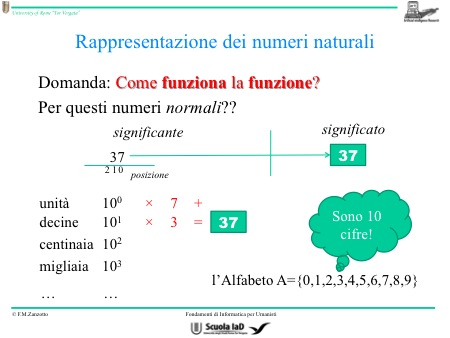
Come si rappresenta la funzione con il numero decimale? Il numero decimale è composto di unità, decine e così via. Per questa funzione bisogna contare i numeri successivi.

Dato che esistono le unità, le decine, le centinaia e…, bisogna calcolare quanto valgono tutte: l’unità vale 1 e così via… perciò, se si pone il 7 di 37 nelle unità, questo numero si leggerà come “ sette”. Il suo valore, infatti, è ottenuto dal fatto che si trova nella posizione delle unità e dal fatto che è “ sette”. La stessa cosa vale per le decine: se prendiamo il 3 di 37 e lo posizioniamo nelle decine, ha il suo valore moltiplicato per 10 in quanto si trova nella posizione delle decine (3 x 10 = 30), quindi il valore di quel numero è 30.

Quindi, la funzione dei numeri decimali è: prendiamo 1 (il valore delle unità) e lo moltiplichiamo per il numero che troviamo nella posizione delle unità (in questo caso 7), poi si moltiplica il valore delle decine (10) per il valore che si trova nella posizione delle decine (in questo caso 3). Il numero che si ottiene in questo caso facendo questo procedimento è 37.

Se determiniamo la posizione, il valore dell’elemento unità, decine, centinaia…, è un numero particolare elevato alla posizione. Partendo dalla posizione 0 che corrisponde alla posizione delle unità, la posizione 1 corrisponde alle decine, la posizione 2 corrisponde alle centinaia, la posizione 3 corrisponde alle migliaia ecc.

La cifra vale valori differenti secondo la posizione in cui si trova.

Perché si ripete il numero 10 (10 elevato alla 0 per la posizione delle unità, 10 elevato alla 1 per la posizione delle decine…)? 10 è il numero delle cifre, ogni cifra, infatti, vale 10 elevato al numero che corrisponde alla posizione in cui si trova.

Questo sistema è legato all’alfabeto, perciò possiamo cambiare il numero di cifre che vogliamo utilizzare, basta che i numeri seguano le stesse regole.

Abbiamo cambiato la base che da 10 è divenuta 2 e interpretiamo il numero 101: 2 elevato alla 0 per la posizione delle unità; 2 elevato alla 1 per le posizioni delle decine; 2 elevato alla 2 per la posizione delle centinaia…

L’alfabeto permette di cambiare la cardinalità. 1 moltiplicato per 2 elevato alla 0 che è 1 è uguale a1; poi moltiplichiamo 0 per 2 elevato alla 1 che è 2, è uguale a 0; poi moltiplichiamo 1 per 2 alla seconda che è 4 e il risultato è 4. perché il significato è 5?

Il valore al numero lo si da come lo si legge. Possiamo cambiare la base poiché i numeri sono legati all’alfabeto. Ma se avessimo B cifre nell’alfabeto, potremo fare lo stesso ragionamento?

Sì. Ci sono popoli che contano in base 24 perché non usano solo le dita delle mani come noi che, infatti, contiamo in base 10. perciò, quella di contare in base 10 è un’imposizione sul sistema, ma il sistema funziona lo stesso se scegliamo un’altra base.

Il caso generale è Val(….) =…

Dato un qualsiasi numero, anche lunghissimo, avrà sempre n cifre. Nel leggere tale numero, già gli si assegna un valore perché lo si legge in decimale, i numeri per quanto lunghi non possono essere infinitamente lunghi. Perciò n è il numero di cifre che compongono il numero.

Nella sommatoria aggiungiamo un nuovo elemento, ovvero i che è un numero generico che può variare tra 0 e n. supponendo che n = 4, i potrà assumere un valore compreso tra 0 e 4. Ciò indica che si possono sommare tutti i numeri da 0 a 4. Perciò i è una variabile che può rappresentare un numero qualunque tra questi.

Partendo da I = 0, vogliamo sommare tutti quei dati per arrivare a I = n. si tratta di una somma di tanti numeri che scriviamo con S (sommatoria).

Per qualsiasi base contenuta nell’alfabeto, si può passare dal significato al significante, avendo una qualsiasi sequenza di simboli.

I numeri che possiamo pensare, sono una qualsiasi sequenza di cifre che vengono descritte da un insieme. La funzione valore funziona in questo modo.

Ciò che abbiamo fatto fin’ora non vale per tutti i numeri, c’è una modalità specifica per ognuno.

Qual è la funzione val?

Per il sistema decimale e per il sistema binario va bene quella vista fin’ora. L’alfabeto, invece, è diverso per ogni numero (naufrago, romano…): decimale A= (0,1, …, 9); binario A = (0,1); romano A = (V, M, c, X, I); naufrago A = (diverso). Il romano e il naufrago sono simili.

Nelle prime due rappresentazioni qualsiasi sequenza di cifre è un numero, cosa che non vale per i numeri romani che sono sequenze di lettere, ma non è che ogni sequenza di lettere rappresenta un numero, e lo stesso anche per il naufrago.