Algoritmi e calcolabilità - Lezione in semi-presenza
| Site: | Università di Tor Vergata for UNWTO |
| Course: | Fondamenti di informatica per il turismo |
| Book: | Algoritmi e calcolabilità - Lezione in semi-presenza |
| Printed by: | Guest user |
| Date: | Friday, 30 January 2026, 6:31 AM |
Description
Lezione in semi-presenza
Table of contents
- 1. Problemi risolubili e algoritmi
- 2. Parametri e Variabili
- 3. Chi è chi nel mondo degli algoritmi: algoritmo, processo, esecutore ed ideatore.
- 4. Esempi di problemi ed algoritmi
- 5. Problemi risolti da più algoritmi
- 6. Algoritmi e realizzazioni meccaniche degli stessi
- 7. Complessità degli algoritmi: scegliere tra algoritmi diversi che risolvono lo stesso problema
1. Problemi risolubili e algoritmi
Per cominciare a capire i mattoni base dell’informatica, bisogna cominciare ad interrogarsi su qual è lo scopo dell’informatica stessa. In un certo senso, lo scopo dell’informatica è cercare di risolvere dei problemi. Certamente, non tutti i problemi saranno risolvibili e, seppur risolvibili, l’intervento umano per trovare la soluzione ci sarà sempre. Non c’è da preoccuparsi. La domanda è dunque: quali tipologie di problemi possono essere trattati? Nel rispondere a tale domanda, ci accorgeremo di due cose:
- trovare questa tipologia di problemi non è affatto un compito difficilissimo
- la definizione dei problemi risolubili sarà intimamente legata alla soluzione che troveremo.
Come promesso, nel trattare ogni argomento, cercheremo di trovare degli esempi e delle nozioni molto vicine alla competenza di base di ogni adulto medio. Nel caso particolare, per definire quali siano i problemi risolubili, prendiamo ad esempio il libro delle elementari dal quale sorgevano spontanei alcuni problemi. Aprendo una pagina a caso, ci si può trovare di fronte a problemini come quello in Figura PROBLEMACONTADINO.
|
Problema Un contadino ha venduto Kg 125 di uva a 0,55 € al chilogrammo e con il ricavo ha acquistato 3 metri di stoffa pagandola 15,80 € al metro. Quale somma gli è rimasta? |
Figura PROBLEMACONTADINO: Un semplice problema
La risoluzione (descritta in Figura SOLUZIONEPROBLEMACONTADINO) è immediata e passa dalla conoscenza delle nozioni di ricavo, somma spesa e somma rimasta.
|
Soluzione 0,55 €/kg´125kg= € 68,75 RICAVO UVA VENDUTA 15,80 €/m´3m= € 47,40 SPESA STOFFA € 68,75- €47,40 = €21,35 SOMMA RIMASTA Risultato finale Al contadino rimangono €21,35 |
Figura SOLUZIONEPROBLEMACONTADINO: La soluzione del semplice problema
Da questo seppur semplice problema con la sua soluzione possiamo ricavare importanti considerazioni. La risoluzione di un qualsiasi problema di questo tipo richiede numerose conoscenze. Conoscere i numeri e le operazioni sugli stessi è indispensabile. Purtroppo, questo non è affatto sufficiente. Per ottenere il risultato finale, occorre infatti sapere o immaginare un procedimento da svolgere. Questo procedimento deve essere pensato per risolvere il problema dato. Ora che abbiamo comunque a disposizione il procedimento di risoluzione, interroghiamoci sulle sue caratteristiche.
Il contadino vende l’uva raccolta e con il ricavato compra una data quantità di stoffa. Siccome la domanda di questo problema è trovare quanto denaro resta in fine al contadino, non posso calcolare per prima la somma rimasta senza calcolare prima il ricavo e la spesa. E’ invece indifferente se prima calcolo il ricavo o la spesa. Il fatto saliente è che la moltiplicazione per sapere quanto ha speso il contadino per comprare la stoffa e la moltiplicazione per sapere quanto è stato il ricavo del contadino per la vendita della sua uva devono essere fatte prima del calcolo della somma rimasta. Quest’ultima operazione può essere svolta solo successivamente. La sottrazione per calcolare quanto denaro è rimasto al contadino (21,35 €) deve avvenire con i termini noti.
Nelle soluzioni a questa tipologia di problemi abbiamo trovato una regolarità. Le soluzioni sono formate da un insieme di operazioni che d’ora in poi chiameremo istruzioni e questo insieme di istruzioni deve essere ordinato. Deve essere possibile scrivere questa sequenza di istruzioni in uno spazio limitato. Quindi, il numero di operazioni nella sequenza risolutiva deve essere finito. Possiamo dunque ora introdurre il termine algoritmo per indicare queste soluzioni. Una prima definizione di algoritmo è la seguente:
Un algoritmo è un insieme ordinato (o sequenza) di istruzioni finito atto a risolvere un problema
oppure (il che è lo stesso)
Un algoritmo è una sequenza finita di passi ( o istruzioni ) atte a risolvere un problema parametrico dato
Possiamo ora rispondere alla domanda iniziale parafrasando in maniera non completamente corretta la tesi di Church: i problemi risolubili sono quelli per i quali sia possibile trovare almeno un algoritmo che possa portare a trovare una loro soluzione. Riportare completamente la tesi di Church è fuori dallo scopo della presente trattazione.
2. Parametri e Variabili
Una caratteristica importante di un algoritmo è che deve essere la soluzione “standardizzata” di una classe di problemi, ovvero uno stessa sequenza finita di passi che risolvono problemi che differiscono soltanto per i dati iniziali (parametri).
Pensiamo ad esempio al problema precedente in Figura 1. Una persona che si confronta con quel problema ha già una procedura in mente e il problema, in genere, viene presentato ai piccoli ed ignari studenti delle elementari come facente parte di una classe di problemi. Lo scolaro deve individuare la classe ed applicare la soluzione standard. Nel caso particolare, la classe di problemi è quella che prevede che qualcuno “ricavi” una somma e ne “spenda” un'altra. La domanda risulta sempre essere quindi la somma rimasta o qualcosa di similare.
Nel caso del determinato problema precedente (Figura PROBLEMACONTADINO), la procedura risolutiva proposta (Figura SOLUZIONEPROBLEMACONTADINO) è invece applicabile solo al particolare problema. Questa procedura risolutiva non può pertanto essere applicata ad altri problemi se non a quello esattamente proposto. Senza arrivare al caso generale in cui è possibile fornire la procedura risolutiva o l’algoritmo per la soluzione della classe dei problemi che prevedono una vendita, un acquisto e il calcolo della somma rimasta, è possibile generalizzare la procedura risolutiva precedente utilizzando il concetto di parametro o variabile. In questo modo, l’algoritmo diventa una procedura risolutiva applicabile ad una classe di problemi e non solo ad un problema specifico dato. Una soluzione più generica al problema precedente è data in Figura SEMPLICEPROBLEMAGENERALIZZATO dove viene generalizzato il problema e la soluzione introducendo le variabili o i parametri. Si osservi anche che la soluzione generalizzata proposta è comunque una procedura risolutiva o un algoritmo in quanto la formula Somma= X*Y-Z*K prevede che vengano fatte prima le moltiplicazioni e poi la sottrazione. Questo non è scritto esplicitamente nella formula ma è un fatto che deriva dalla conoscenza della precedenza degli operatori ovvero che la moltiplicazione deve essere fatta prima delle operazioni di somma e sottrazione. L’ordine di precedenza degli operatori ci pare una cosa naturale ma non lo è. Qualcuno ha deciso la convenzione e ce la fa trasmettere attraverso le nozioni che nel corso della nostra vita ci vengono fornite.
|
Problema Generalizzato Un contadino ha venduto Kg X di uva a Y € al chilogrammo e con il ricavo ha acquistato Z metri di stoffa pagandola K € al metro. Quale Somma gli è rimasta? Procedura Generalizzata Somma= X*Y-Z*K |
Figura SEMPLICEPROBLEMAGENERALIZZATO Semplice problema generalizzato e relativa soluzione
Comunque, la generalizzazione del problema e della procedura risolutiva rende la soluzione applicabile per tutti i problemi che sono formulati con le stesse parole di quelle del problema generalizzato in Figura SEMPLICEPROBLEMAGENERALIZZATO e dove al posto delle X, Y, Z e K si trovano dei numeri. In un certo senso, il problema generalizzato è una maschera con dei buchi. Se la maschera può essere sovrapposta al problema attuale, allora il problema è risolubile con la procedura generalizzata espressa.
Con la parametrizzazione di un problema trovo quindi una soluzione che risolve piu’ problemi fra loro simili, che differiscono soltanto per le informazioni iniziali (parametri).
Ma in realtà si può osservare che una soluzione (algoritmo), può essere valida per differenti problemi.
Se si riesce a trovare l’algoritmo che può risolvere più di un problema, si può fornire tale “ricetta” a qualcun altro, a chi ne ha bisogno.
Facendo riferimento sempre al problema dell’uva e della stoffa, non è importante la figura del contadino, non è importante neppure l’uva, come è indifferente l’azione di comprare stoffa. La cosa importante è l’esistenza di una persona che vende e acquista.
La sequenza "naturale" delle operazioni e degli operatori, è una cosa che qualcuno ha deciso, una convenzione. Perciò si seguono anche procedure in modo standardizzato. Queste procedure che ci sono state insegnate, hanno passaggi ben precisi.
L’algoritmo prevede di svolgere le operazioni secondo la precedenza degli operatori. L’unico modo per violare la precedenza degli operatori è mettere le parentesi. Queste operazioni le svolgiamo anche in un determinato modo, ovvero da sinistra verso destra poiché è il nostro modo di scrivere.
Come si fa a prendere come standard questa soluzione (algoritmo)?
Cambiando i numeri con delle variabili. Ad ogni variabile è assegnato un determinato valore.
Una variabile è il nome di uno spazio mentale o di uno spazio qualsiasi. In questo spazio vi si può porre un valore. La variabile è il nome dello spazio (ad x posso far assumere il valore di 4 ma anche di 5, ecco perché si tratta di uno spazio mentale). È lo spazio che varia il valore, non la variabile.
La variabile è formata da: un nome e uno spazio ad esso associato. Lo spazio deve assumere un valore. Se ponessimo lo stesso nome in due parti diverse, ci riferiremmo allo stesso spazio di memoria che abbiamo in testa. Non si tratterebbe di spazi differenti anche se nella scrittura risultano due spazi differenti.
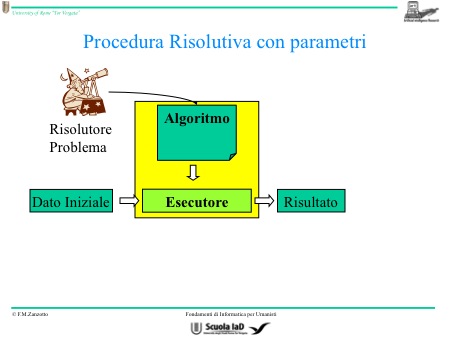
Le variabili d’ingresso prendono il nome di parametri. Si è compreso che vi è un altro elemento che si può variare, ovvero il dato iniziale.
Variabili d’ingresso = parametri = dati iniziali = valori iniziali della variabile.
Possiamo variare se mettiamo i valori appositi negli spazi appositi. Così facendo si è aumentata la quantità di problemi che riusciamo a risolvere con una sola soluzione.
A questo punto, riusciremo a risolvere tutti i problemi che rientrano in quel caso generale. Problemi che, in un certo senso, risultano infiniti perché i numeri possono variare infinitamente. Quest’infinitezza non ci aiuta nel dire che si possono risolvere tutti i problemi di quel caso generale. Inoltre, questo meccanismo, si può generalizzare ulteriormente, così che si potranno risolvere ulteriori problemi. Si arriva quindi all'unificazione: prendo una variabile e "ci metto lo schema" (ovvero la sequenza finita di istruzioni) che mi serve per risolvere il problema.
Ciò che deve restare invariata è l’unità di misura (metri, euro…).
L’operazione di unificazione consiste nel prendere una variabile, mettere lo schema sul problema reale, e si ottiene che 125 (kg d’uva venduta) è unificato ad x. Finisce nello spazietto di memoria occupato da x.
3. Chi è chi nel mondo degli algoritmi: algoritmo, processo, esecutore ed ideatore.
I numeri (i dati del problema), le operazioni da svolgere (quella per conoscere la spesa, quella per conoscere il ricavo…), il procedimento da svolgere.
La macchina non può trovare una soluzione possibile a un problema poiché essa è un elemento che non ragiona.
Il procedimento da svolgere per risolvere il problema, non è immediato poiché prima bisogna comprendere il testo. Una volta scritta la procedura risolutiva, essa può essere risolta anche da un individuo che conosca solo le operazioni. Esiste, perciò, un momento in cui qualcuno costruisce la procedura risolutiva, e un momento in cui, un secondo qualcuno la esegue. In alcuni casi, queste due figure possono rivelarsi una figura sola (ad esempio lo studente che deve risolvere un problema di matematica o geometria).
Parlando dei teoremi ad esempio, la dimostrazione è una procedura risolutiva?
Si tratta sempre di una sequenza di passi, ma non vi sono i due ruoli, perché non c’è un individuo che produce la dimostrazione e un altro che la esegue, poiché, una volta data non si deve risolvere. Può darsi che ci sia qualcuno che deve riscoprirla, ma si tratta sempre di riscoprire la dimostrazione. In questo caso, quindi non ci sono i due ruoli.
Tornando alla sequenza di operazioni viste finora, chi svolge la serie di operazioni può essere un individuo distinto e con meno capacità intellettuali di colui che deve svolgere l’atto creativo necessario affinché si trovi la soluzione al problema.
Cos’è l’atto creativo? Per trovarlo occorre un “creatore”. Ma, se si tratta di una procedura già esistente, la persona che la svolgerà può anche non avere le capacità creative.
Esiste un intermezzo tra chi trova la soluzione e chi la esegue che è la serie di istruzioni. Serie di istruzioni che prende il nome di algoritmo.
Questa serie di istruzioni è la soluzione ad un particolare problema proposto. Non si tratta di una sequenza astratta, ma è adibita a risolvere un determinato problema.
Se si osserva esclusivamente l’insieme delle istruzioni, vediamo che, in un certo senso, non è esclusivamente la soluzione del problema, ma è un modo per ottenere la soluzione del problema stesso. Per ottenere questa soluzione, occorre qualcuno che la prepari. Che, cioè, svolga tali operazioni usando le proprie competenze.
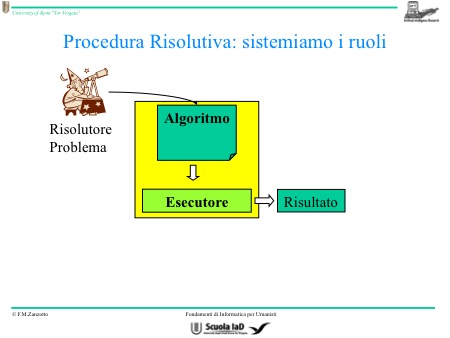
Esistono due fasi distinte: l’algoritmo (fase 1) e l’esecuzione dell’algoritmo (fase 2). L’esecuzione dell’algoritmo viene detta processo.
L’algoritmo è quindi una modalità di risoluzione del problema, tale modalità di risoluzione ha specifiche caratteristiche poiché si tratta di una sequenza di istruzioni.
L’esecutore non ha le stesse competenze di colui che trova la risoluzione del problema, ma ha altre competenze, ovvero di poter eseguire quell’algoritmo. Una volta che termina l’esecuzione dell’algoritmo, ottiene il risultato.
Si ha un foglio (algoritmo) dove sono scritte le istruzioni, e qualcuno che legge il foglio e risolve il problema tramite quelle istruzioni. Questo secondo individuo, quando legge il foglio, cambia la sua memoria e trasforma le informazioni che ha in altre informazioni. Si ha un elemento aggiuntivo: foglio, esecutore del foglio, memoria dell’esecutore. Trasformando la sua memoria, l’esecutore ottiene un risultato.
4. Esempi di problemi ed algoritmi
Anche una ricetta è un algoritmo, ma una ricetta è parametrica, cioè, ha delle variabili iniziali?
In un certo senso sì, la ricetta è parametrica perché dipende per quante persone devo cucinare.
Il menù di un ristorante è un algoritmo? È una sequenza ma non è un algoritmo. Al contrario, un menù fisso è un algoritmo perché il cameriere sa che, seguendo quell’ordine, deve portare determinate portate. Quindi un menù fisso è un algoritmo perché è una dichiarazione di una procedura.
La lista della spesa è un algoritmo? No perché se non prendo le cose al mercato nell’ordine in cui le ho scritte sul foglio, non accade nulla.
Un algoritmo quindi è una sequenza di istruzioni atte a risolvere un problema parametrico dato.
Una ricetta è praticamente sempre un algoritmo. Una ricetta è parametrica?
Data una ricetta produce sempre lo stesso dolce.
Le ricette sono procedure, sequenze di operazioni, alcune sequenze non si possono invertire o saltare quindi si tratta di algoritmi.
Anche lo spartito musicale è un algoritmo. Ma è parametrico?? ???...in un certo senso a volte sì, poiché l'esecuzione dipende dalla velocità metronomica (quando non è indicata direttamente nello spartito),tuttavia vi sono altri fattori che non potremmo definire parametrici, perché non variano in maniera proporzionale.
Ma la ricetta è parametrica? In un certo senso sì perché può variare la quantità di persone…
Riprendendo dalla lezione precedente, avevamo iniziato a parlare delle operazioni. Per prima cosa avevamo visto cos’è un problema e quando è risolvibile, poi avevamo visto che esiste il concetto di soluzione del problema che abbiamo riconosciuto come un algoritmo, e poi abbiamo visto che, per risolvere un problema, esistono diversi ruoli.
Per risolvere un problema abbiamo bisogno di un algoritmo e di un esecutore. Quindi i ruoli saranno: colui che ha creato l’algoritmo che serve affinché il problema venga risolto, e l’esecutore ovvero colui che deve eseguire il problema. L’esecutore segue l’algoritmo e lo svolge ovvero fa il processo. Il processo non è altro che una sequenza di passi attuata da qualcuno, non prima, però, che l’algoritmo sia stato scritto.
Si richiede anche l’esistenza di un individuo che pensi l’algoritmo. Un individuo creativo, più “geniale” degli altri poiché ha pensato l’algoritmo stesso. Visto ciò, ci siamo soffermati sulla capacità risolutiva dell’algoritmo stesso, ovvero: l’algoritmo individuato inizialmente poteva risolvere un solo problema, o almeno così noi pensavamo. In realtà, introducendo il concetto di variabile, si ha a disposizione una serie di algoritmi che risolvono una serie di problemi (problemi che sono molto simili tra loro).
Un algoritmo è una sequenza di istruzioni atte a risolvere un problema parametrico dato.
Si vedrà il problema della somma, il problema della moltiplicazione e il problema del MCD (massimo comun divisore).
5. Problemi risolti da più algoritmi
Sommare due numeri
La somma: dati due numeri, bisogna sommarli. Per svolgere una somma, si possono utilizzare due metodi. Il metodo più semplice, che viene insegnato ai bambini molto piccoli (prima elementare) perché è più facile da comprendere, è il metodo del pallottoliere.
Somma e addizione sono due sinonimi. L’operazione della somma consiste nel mettere insieme due elementi (una certa somma di sassi e un’altra certa somma di sassi). Il risultato che otterremo da quest’unione sarà il risultato della somma, quindi da due numeri, ne avremo solo uno.
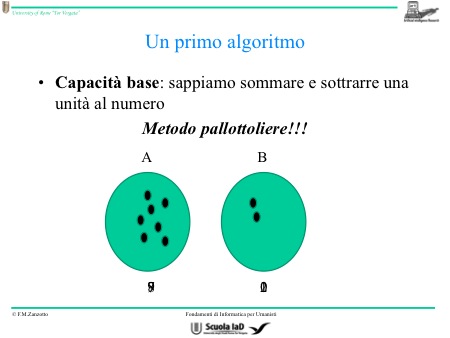
Metodo del pallottoliere
Tornando al metodo del pallottoliere, abbiamo due insiemi di sassi, A e B. in A ci sono 7 sassi e in B ci sono 2 sassi. Per fare la somma tra A e B, usando il metodo del pallottoliere, si comincerà sottraendo un sasso a B per metterlo in A. in questo passaggio vediamo quindi che A contiene 8 sassi e B ne contiene 1. ma la somma non è finita, ripetiamo il procedimento precedente così che in A vi saranno 9 sassi e in B 0. la somma è terminata e il risultato è 9.
Questo si chiama metodo del pallottoliere perché il pallottoliere sposta una pallina alla volta. Questo procedimento è particolare perché non abbiamo sommato A e B per ottenere un risultato in C (ad esempio), ma abbiamo sottratto a B e aggiunto ad A per ottenere il risultato in A.
Non si tratta della normalità di quando descriviamo una somma che sarebbe piuttosto: sette più due è uguale a nove (7 + 2 = 9).
L’algoritmo del pallottoliere si ha quando: per prima cosa la capacità base è saper sommare e sottrarre un’unita. A e B sono i due numeri che voglio sommare, perciò si metterà in A ciò che si ottiene facendo A + 1 e in B ciò che si ottiene facendo B – 1. se B non è uguale a 0 si deve ripetere il procedimento. In questo caso si deve ripetere due volte prima che B sia 0. quando B è 0 vediamo che A contiene la somma tra l’originale A (in questo caso 7) e l’originale B (in questo caso 2).
E’ un algoritmo perché si tratta di una sequenza di istruzioni finita perché la posso scrivere in un foglio finito (o più fogli). Su questi fogli ci sono le istruzioni o operazioni, che sono una dopo l’altra.
Algoritmo “normale”
Ma c’è anche un altro algoritmo per sommare due o più numeri ovvero quello che noi oggi definiamo “normale”. Anche qui lo definiremo tale in quanto è quello che ci viene generalmente insegnato per svolgere una somma. Come si deve procedere?
Prendendo i due numeri, A e B, si mettono i due numeri in colonna ovvero B allineato sotto ad A o viceversa. Allineati di modo che le unità coincidano e così via. Una volta fatto ciò si traccia la linea sotto all’ultimo numero, si scrive un = e si comincia lo svolgimento.
Si comincerà dalla colonna più a destra che chiameremo colonna attiva e li sommiamo. Se la somma supera 10 dovremo usare il riporto. L’uno del riporto lo scriveremo più piccolo, in alto, accanto alla colonna delle decine. Poi si sommano anche le decine con eventuale riporto e così avremo il risultato per intero.
Anche questo è un algoritmo. La capacità-base di quest’algoritmo è saper contare fino a 10. oggetti conoscitivi che già avevamo in mente, si chiamano algoritmi. Ovviamente, quando abbiamo finito con la colonna delle unità, la colonna attiva si sposta verso sinistra e poi via via che l’algoritmo procede.
Abbiamo così terminato il problema della somma e abbiamo visto che vi sono due algoritmi per risolverlo (anche se se ne potrebbero inventare altri). Ma perché sono due? Qual è il migliore dei due? Come scegliamo tra i due?
Moltiplicare due numeri
Algoritmo del pallottoliere
Altro problema: dati due numeri A e B, dobbiamo moltiplicarli. Avremo anche qui due algoritmi. Ma se sapessimo solo sommare, come potremo operare? Abbiamo 3 colonne, A, B e C. sotto A c’è il numero che vi corrisponde, sotto B c’è il numero che vi corrisponde e sotto C ci scriveremo il risultato.
Nel primo passo C è 0. cominciamo, per ogni passaggio, a diminuire B di un’unità e, ogni volta che lo facciamo, aggiungiamo in C il valore di A. alla fine avremo il numero A moltiplicato il numero B in C.
E’ uguale all’algoritmo della somma chiamato pallottoliere, con l’aggiunta di C.
Algoritmo “normale”
Però c’è un altro algoritmo per fare la moltiplicazione, ovvero quello in cui operiamo diversamente. Abbiamo sempre A e B e, ponendoli uno sotto l’altro, iniziamo a fare la moltiplicazione. Per svolgere velocemente quest’operazione, occorre saper svolgere rapidamente la capacità base, bisogna cioè sapere le tabelline.
Algoritmi e realizzazioni meccaniche degli stessi
Nel procedere, ne esistono una miriade di questi algoritmi, alcuni ci sono stati insegnati e altri li hanno tralasciati. Il concetto di algoritmo, così come ci è stato insegnato, esiste già da tempo così come, le macchine non le abbiamo pensate noi nel XX secolo. L’elemento algoritmico più antico che l’umanità abbia avuto è l’orologio. Esso realizza un algoritmo particolare ovvero quello di misurare il tempo. Misura le ore e i minuti (ma anche i secondi) attraverso due lancette: quella più lunga dei minuti e quella più corta delle ore. Ad ogni giro intero della lancetta dei minuti, la lancetta delle ore fa un passo in avanti.
Pascal pensò ad altre macchine partendo dall’algoritmo della somma. Non è oggi che sono stati scoperti gli algoritmi e neppure oggi che essi sono stati applicati a delle macchine, semplicemente la tecnologia è avanzata.
Il problema che risolve l’algoritmo può essere parametrico. L’algoritmo è una cosa distinta rispetto all’esecuzione dello stesso e all’invenzione dello stesso.
Perché un algoritmo è finito? Perché può essere scritto in un tempo finito, non può essere infinito. Infinito, invece, può essere un processo. Deve essere possibile scrivere l’algoritmo che per questo deve essere contenibile in uno spazio finito. Dall’altra parte, l’esecuzione di un algoritmo, può durare all’infinito poiché un processo può durare all’infinito.
L’algoritmo è una sequenza di istruzioni, mentre il processo è una sequenza di passi. Un passo è lo stato della variabile A e della variabile B. ad esempio, per sommare 45 e 63, bisognerà fare un certo numero di passi.
Anche per mettere a posto dei fogli si adotta una procedura. Possono essere usate diverse procedure, diversi algoritmi. Il migliore è quello più veloce, quello che se applicato impiega meno tempo.
6. Algoritmi e realizzazioni meccaniche degli stessi
Nel procedere, ne esistono una miriade di questi algoritmi, alcuni ci sono stati insegnati e altri li hanno tralasciati. Il concetto di algoritmo, così come ci è stato insegnato, esiste già da tempo così come, le macchine non le abbiamo pensate noi nel XX secolo. L’elemento algoritmico più antico che l’umanità abbia avuto è l’orologio. Esso realizza un algoritmo particolare ovvero quello di misurare il tempo. Misura le ore e i minuti (ma anche i secondi) attraverso due lancette: quella più lunga dei minuti e quella più corta delle ore. Ad ogni giro intero della lancetta dei minuti, la lancetta delle ore fa un passo in avanti.
Pascal pensò ad altre macchine partendo dall’algoritmo della somma. Non è oggi che sono stati scoperti gli algoritmi e neppure oggi che essi sono stati applicati a delle macchine, semplicemente la tecnologia è avanzata.
Il problema che risolve l’algoritmo può essere parametrico. L’algoritmo è una cosa distinta rispetto all’esecuzione dello stesso e all’invenzione dello stesso.
Perché un algoritmo è finito? Perché può essere scritto in un tempo finito, non può essere infinito. Infinito, invece, può essere un processo. Deve essere possibile scrivere l’algoritmo che per questo deve essere contenibile in uno spazio finito. Dall’altra parte, l’esecuzione di un algoritmo, può durare all’infinito poiché un processo può durare all’infinito.
L’algoritmo è una sequenza di istruzioni, mentre il processo è una sequenza di passi. Un passo è lo stato della variabile A e della variabile B. ad esempio, per sommare 45 e 63, bisognerà fare un certo numero di passi.
Anche per mettere a posto dei fogli si adotta una procedura. Possono essere usate diverse procedure, diversi algoritmi. Il migliore è quello più veloce, quello che se applicato impiega meno tempo.
7. Complessità degli algoritmi: scegliere tra algoritmi diversi che risolvono lo stesso problema
L’algoritmo migliore per riordinare i fogli è quello di fare dei mucchietti perché divide il problema in tante parti. Poi analizza e risolve ogni parte e in fine le mette insieme e trova la soluzione del problema.
Perché quand’eravamo bambini, e poi quando siamo cresciuti, ci hanno insegnato un algoritmo in particolare (ad esempio per risolvere la somma) e non l’altro?L’algoritmo del pallottoliere viene generalmente insegnato ai bambini piccoli perché è più semplice da comprendere e più divertente da svolgere se vogliamo. Solo qualche anno dopo gli viene insegnato l’algoritmo “ normale” per risolvere la somma.
Il metodo del pallottoliere è più semplice, ma, la differenza sostanziale non è la semplicità, oppure si direbbe che il metodo da scegliere, quello più conveniente, è quello del pallottoliere. Al contrario, il metodo più conveniente per risolvere un problema è quello “ normale” perché la differenza sta nel tempo impiegato per risolvere il problema con entrambi i metodi; importante è misurare l’aspettativa del tempo richiesto per risolvere un problema. Anche se, come abbiamo detto, può essere infinito.
Usando il metodo del pallottoliere, immaginando che dovessimo sommare 45 e 63, dovremmo fare 63 passi. Nel caso generale, se dobbiamo sommare 2 numeri, A e B, usando il metodo del pallottoliere, dovremo fare B passi. Usando il metodo “ normale”, vediamo che i passi sono due, infatti, c’è n + 1, lì dove n sono le cifre di B.
N è di solito minore di B: se B è uguale a 50, N è uguale a 2. quindi il secondo algoritmo per risolvere la somma (l’algoritmo “ normale”) è più veloce.
Se quindi ci fermiamo ad osservare gli algoritmi in sé, sicuramente il giudizio sarà che il più conveniente, in quanto più semplice, è quello del pallottoliere, ma se osserviamo i processi, ci rendiamo conto che l’algoritmo migliore è quello della somma tradizionale (quello che ci viene insegnato).
Il problema sta nelle parole perché. Un passo è un’operazione base. Passi è l’operazione base che viene ripetuta tutte le volte ovvero saper sommare e sottrarre un numero tutte le volte.
Il passo del secondo algoritmo è più complesso perché bisogna sommare due cifre all’istante. Si tratta, quindi, di due capacità-base differenti.
Si riesce a arrivare dai passi-pallottoliere ai passi normali? Si, ma per fare 1 passi normale occorre fare 9 passi del pallottoliere. Allora i passi del pallottoliere non convengono eppure c’è ancora oggi qualcuno che conta con le mani.
Era l’argomentazione che era sbagliata, l’argomentazione per convincere che il secondo algoritmo è migliore di quello del pallottoliere.
Il criterio per scegliere un algoritmo è quello che risolve il problema, una volta che abbiamo appurato che due algoritmi risolvono lo stesso problema, si sceglie quello più veloce.
Per scegliere l'algoritmo migliore si deve individuare l'esecuzione più rapida e tenere in considerazione:
- come è scritto l'algoritmo ovvero quali sono le istruzioni (comprensibilità e numero d'istruzioni)
- osservare le ipotetiche istruzioni ovvero i possibili processi (i numeri di passi da fare).